Isosceles Tutorial: Inscribing a Triangle

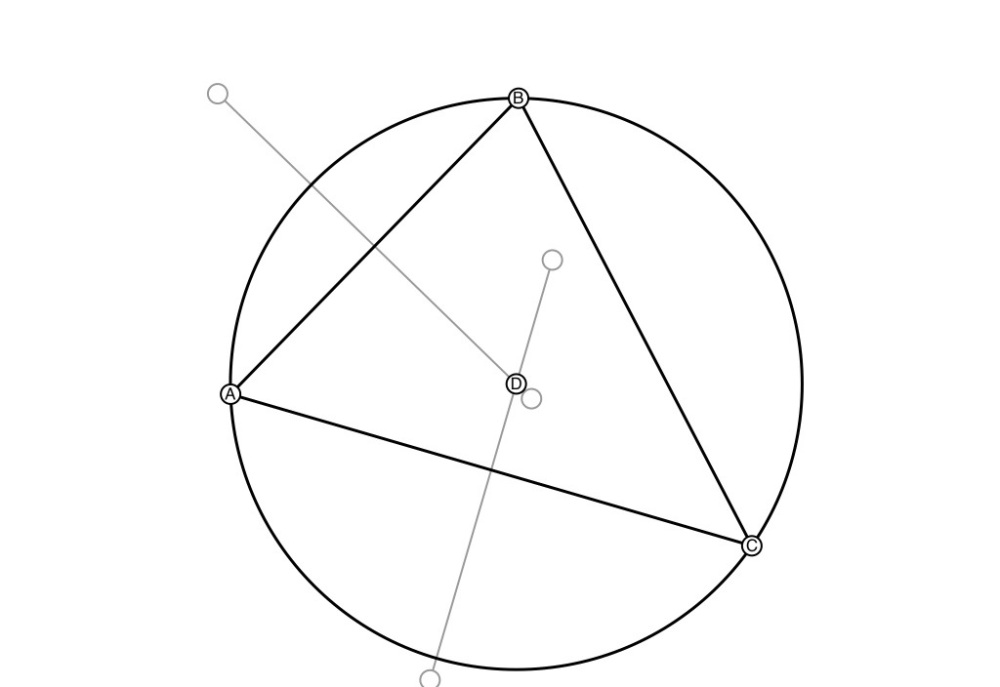
Inscribing a circle in a triangle is finding a circle that is precisely tangent to each of the sides of the triangle. To do this we first find the incenter, which is the intersection of the bisectors of each angle in the triangle.

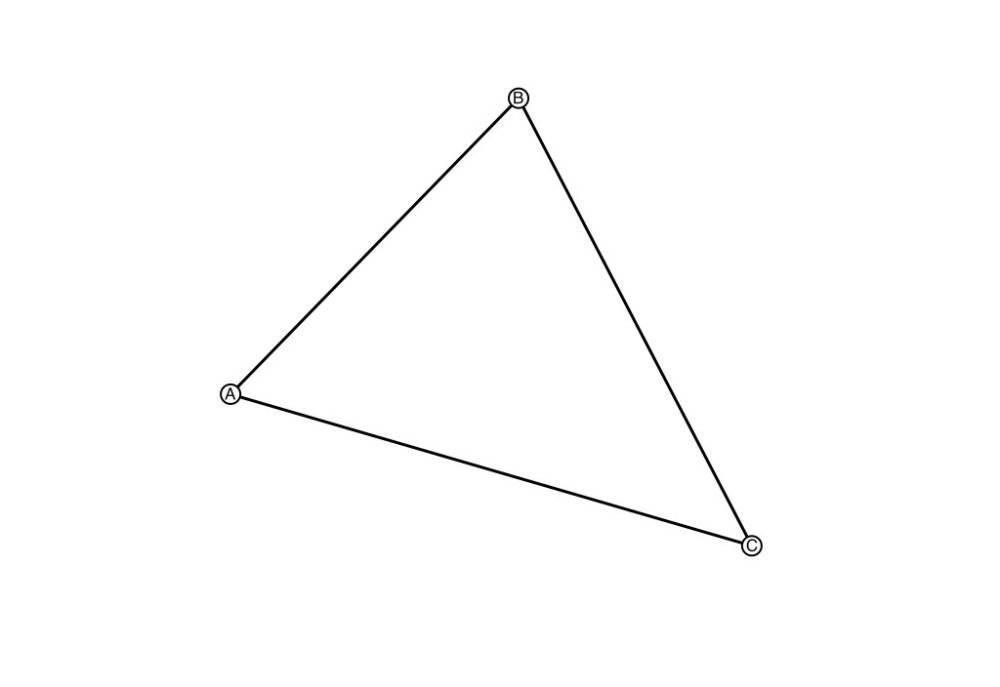
1. Create a point to start the triangle.

2. Draw a line from the point by dragging from it with the Line tool selected.

3. Draw more lines to finish the triangle.

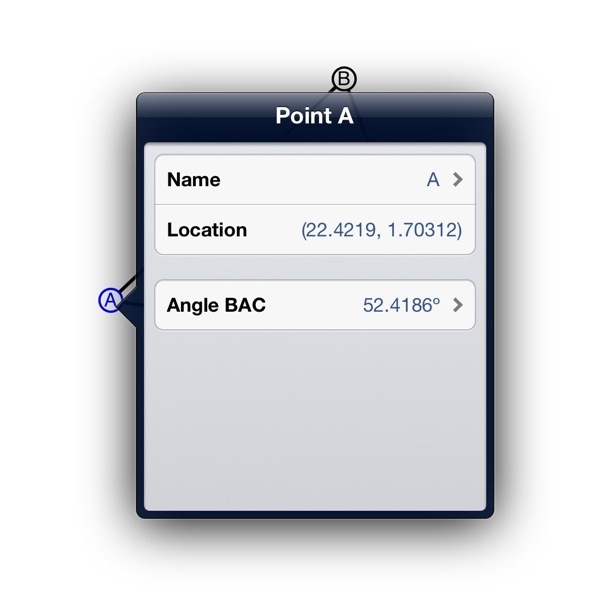
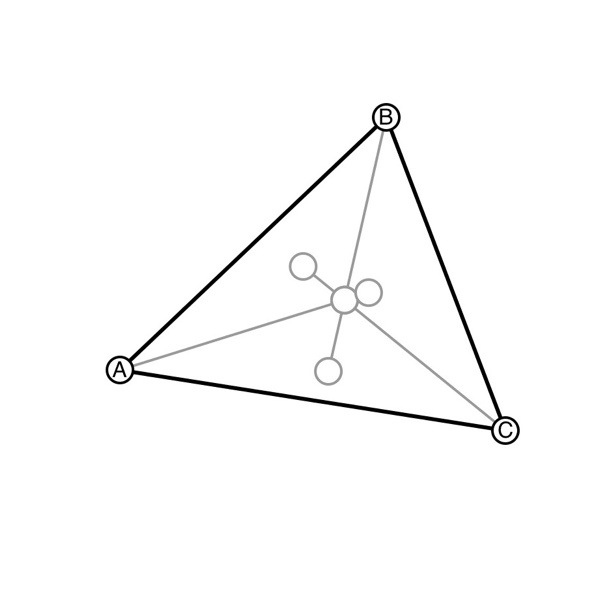
4. To construct the angle bisector traditionally, we could use the compass tool. However, there is a shortcut in Isosceles to do this. First tap and hold on a point, and tap Info in the menu that appears. You should see a menu like this:

5. Tap the angle item in the menu, then tap Construct Bisector. The bisector will appear on the canvas.

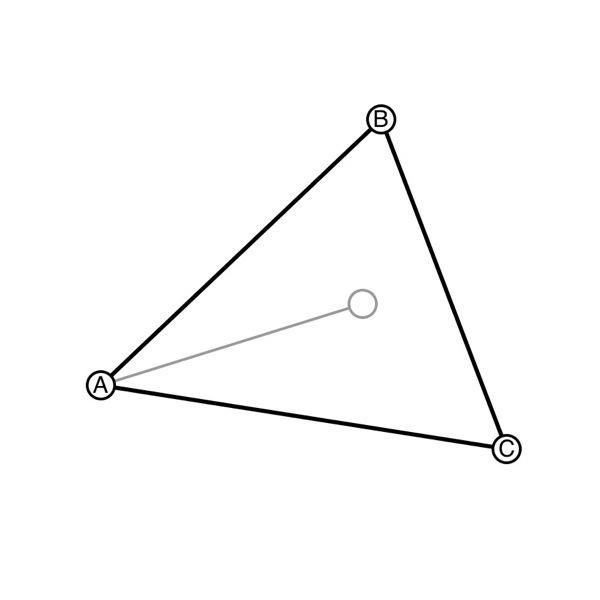
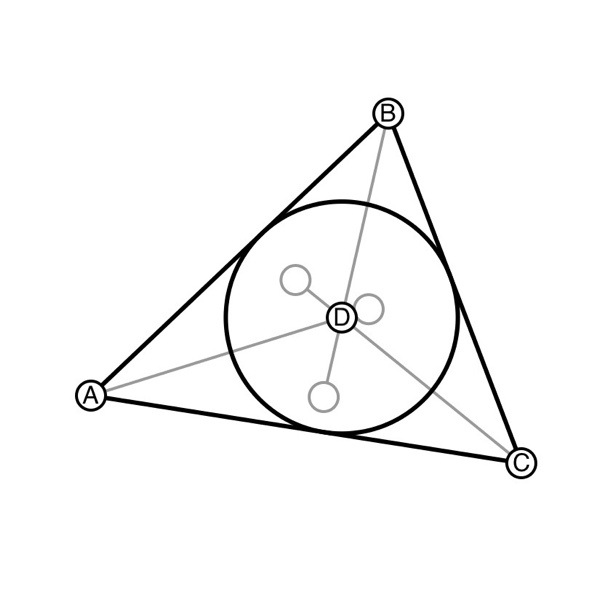
6. Repeat the process for all the points in the triangle. If you have Shows Intersections turned on in the Canvas settings, you should already see the intersection of the bisectors.

7. Tap the intersection with the default pencil selected to create the incenter. Using the Circle tool, you can now create the circle that is tangent to the sides of the triangle.

I hope this helped you make the most of Isosceles! Please leave a comment if you have any questions, or contact me from the Help menu in the app.

Triangle Centers: Circumcenter

Moving forward from perpendicular bisectors, let’s talk about a topic you’ll certainly see in a geometry course: triangle centers.

If you Google “triangle centers“, you’ll find that there are actually compiled indexes of these creatures – they number in the hundreds at least. In fact, there are so many that they have to be named using alphanumeric codes! To keep this site from turning into another exhaustive list, we will cover the four triangle centers that are by far the most common ones you will see.

Part 1: Circumcenter

Hint: We’ll need our knowledge from the last post on perpendicular bisectors to figure out this triangle center.

The circumcenter is the point on the triangle that is equidistant from each of the triangle’s vertices. To put it another way, the lines connecting the circumcenter and each vertex are the same length. So we can say that the circumcenter is the center of a circle (aptly named the circumcircle) that passes through the triangle’s vertices. In the figure below, D is the circumcenter and the center of the circumcircle.

We’re given a triangle, like this:

How does one construct a circumcenter? Remember, we’re looking for a point that is equidistant from the triangle vertices. As it happens, any point equidistant from the vertices of a line is on the perpendicular bisector of that line. (Recall the arcs drawn in the last post.) So let’s find the perpendicular bisectors of two of the triangle sides (three, if you want, but you only need two lines to find an intersection).

In this diagram, we have constructed the perpendicular bisectors of AB and AC. Any point on the bisector of AB is equidistant from A and B, and any point on AC’s bisector is equidistant from A and C. Logically, if we take the intersection of the two bisectors D, then D is equidistant from A, B, and C. Therefore, D is the circumcenter of triangle ABC.

To summarize: The circumcenter of a triangle is the intersection of two of the triangle’s perpendicular bisectors because the intersection is equidistant from each of the vertices of the triangle.

NEW: If you have a copy of Isosceles on your iPhone, iPod touch, or iPad, you can download the Isosceles GSK file from this post and explore circumcenters on your own. Tap here on your device to download the file.

If this helped you understand perpendicular bisectors, or if you have any questions, please post a comment below. Next time we’ll discuss another triangle center, the incenter.